RE - MATE
sábado, 1 de diciembre de 2018
viernes, 30 de noviembre de 2018
Presentación de la Parábola
Definición
Una parábola se define como el conjunto de puntos en el plano que se encuentran a una misma distancia de un punto fijo llamado Foco y una línea recta también fija llamada Directríz.
Al punto medio entre el foco y la directriz se le conoce con el nombre de Vértice.
La recta que pasa por el foco y es perpendicular a la directriz, es decir su intersección forma un ángulo recto, se le conoce con el nombre de Eje de simetría
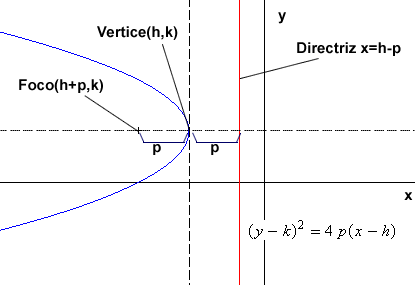 La ecuación para una parabola con eje focal paralelo al eje y, vertice en (h,k) y cuya distancia al foco es p es:
La ecuación para una parabola con eje focal paralelo al eje y, vertice en (h,k) y cuya distancia al foco es p es: 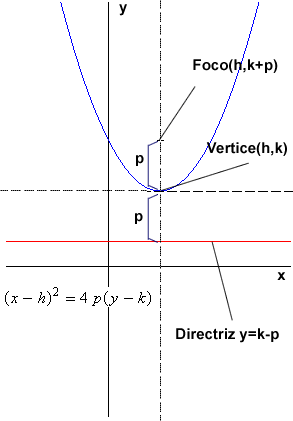
Una parábola se define como el conjunto de puntos en el plano que se encuentran a una misma distancia de un punto fijo llamado Foco y una línea recta también fija llamada Directríz.
Ecuación de una parábola
La ecuación para una parabola con eje focal paralelo al eje x , vértice en (h,k) y cuya distancia al foco es p es:


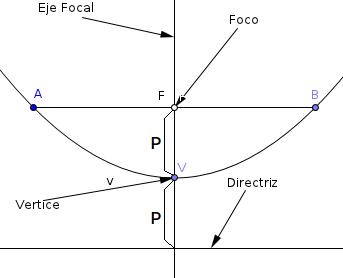
Elementos de la parábola
Directriz
La Directriz es la recta sobre la cual si medimos su distancia hasta un punto cualquiera de la parábola, esta debe ser igual a la distancia de este mismo punto al Foco
Eje Focal
El eje focal es la recta perpendicular a la directriz que pasa por el foco.
Vértice
Es el punto en el cual la parábola corta el eje focal.
Lado Recto
Es un segmento paralelo a la directriz, que pasa por el foco y es perpendicular al eje focal y sus extremos son puntos de la parabola(A,B).
Parámetro
La distancia entre el vertice y la directriz que es la misma denter el vertice y el focode una parábola recibe el nombre de parámetro de la parábola (suele denotarse por p).

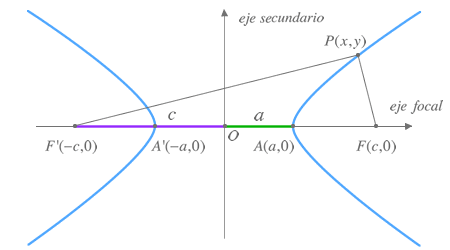
Presentación de la hipérbola
Dados dos puntos F1 y F2 llamados focos, se denomina hipérbola al conjunto de puntos del plano tales que el valor absoluto de la diferencia de sus distancias a los focos es constante.
Elementos de la Hipérbola
Los elementos de la hipérbola son:

1. Focos: Son los puntos fijos F y F'.
2. Eje principal o real: Es la recta que pasa por los focos.
3. Eje secundario o imaginario: Es la mediatriz del segmento FF'.
4. Centro: Es el punto de intersección de los ejes.
5. Vértices: Los puntos A y A' son los puntos de intersección de la hipérbola con el eje focal. Los puntos B y B' se obtienen como intersección del eje imaginario con la circunferencia que tiene por centro uno de los vértices y de radio c.
6. Radios vectores: Son los segmentos que van desde un punto de la hipérbola a los focos: PF y PF'.
7. Distancia focal: Es el segmento  de longitud 2c.
de longitud 2c.
8. Eje mayor: Es el segmento  de longitud 2a.
de longitud 2a.
9. Eje menor: Es el segmento  de longitud 2b.
de longitud 2b.
10. Ejes de simetría: Son las rectas que contienen al eje real o al eje imaginario.
11. Asíntotas: Son las rectas de ecuaciones: 
12. Relación entre los semiejes: 
Hipérbola equilatera
La hipérbola equilátera es la que tiene sus asíntotas (A1 y A2) perpendiculares entre sí, o, dicho de otra manera, cuando forman un ángulo con cada eje de 45º.

Relación entre semiejes de la hipérbola
Las semiejes de la hipérbola (a y b) se relacionan con la distancia focal (c) por la siguiente fórmula:
Geométricamente podemos encontrar los puntos B1 y B2. Para ello, se trazan las rectas tangentes a la hipérbola en los vértices V1 y V2. Las dos tangentes cortarán en las asíntotas en cuatro puntos. Unimos los segmentos dos a dos siendo de longitud 2a y perpendicular al eje no transverso. Los dos puntos producto de la intersección de los dos segmentos y el eje no transverso serán B1 y B2. Siendo O=(o1,o2) el centro de la hipérbola, tendremos que B1=(o1,o2+b) y B2=(o1,o2-b).
De esta forma, se podría calcular el semieje imaginario (b) a partir del semieje real (a) y la semidistancia focal (c):
Ecuación canónica de la hipérbola

Es la ecuación canónica de la hipérbola con centro en (0,0) y eje focal y=0 (eje x)
Excentricidad de la hipérbola
La excentricidad mide lo “abierta” que es la hipérbola. Puesto que c(semidistancia focal) es siempre mayor que a (semieje real), la excentricidad de la hipérbola es siempre mayor que la unidad.

Casos particulares de las hipérbolas
Si las hipérbolas se encuentran centradas en el origen de coordenadas, las ecuaciones anteriores se pueden reducir considerablemente ya que x0=0 e y0=0. Teniendo en cuenta este hecho:
Hipérbola de eje focal horizontal centrada en el origen
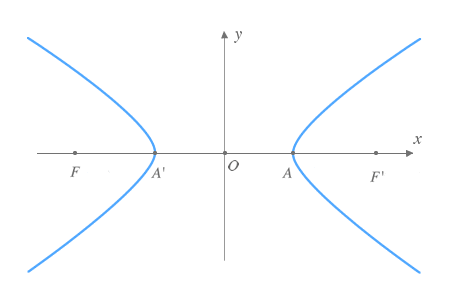
La ecuación de una hipérbola de eje focal horizontal centrada en el origen viene dada por:
Donde:
- a : Semieje real
- b : Semieje imaginario
Hipérbola de eje focal vertical centrada en el origen
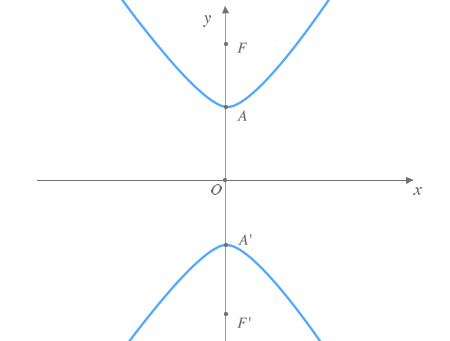
La ecuación de una hipérbola de eje focal horizontal centrada en el origen viene dada por:
Donde:
- a : Semieje real
- b : Semieje imaginario
martes, 13 de noviembre de 2018
Suscribirse a:
Comentarios (Atom)